A friend recently introduced me to a new coding puzzle. This led to a new algorithm that I hadn’t seen before. As usual while figuring out I came up with several mad approaches, so I thought I’d write them down and see if they showed anything about the way my brain works.
The Problem:
Given an array of integers, for each calculate the result of multiplying all the other entries in the original array except the current entry.
Oh, and you can’t use the division operator.
Oh, and it’s possible in linear time i.e. there’s a solution which is O(n).
Hmmm.
If you want to try it yourself look away now.
Solution 1: Brute-force
So obvious brute-force solution is O(n^2).
// For each index, scan whole array and multiply all but this one together.
public int[] CalcProductsNSquared(int[] input)
{
int[] products = new int[input.Length];
for ( int i = 0; i < input.Length; ++i )
{
products[i] = CalculateSimpleAllButOneProduct(input, i);
}
return products;
}
private int CalculateSimpleAllButOneProduct(int[] input, int iSkip)
{
int product = 1;
for (int j = 0; j < input.Length; ++j)
{
if (j != iSkip)
{
product *= input[j];
}
}
return product;
}
Solution 2: Divide and conquer
Then my brain wandered to the other restriction. Why can’t I use division, what happens if I do? Then you get a nice easy and fast O(n) solution. So that’s why we can’t use division – it’s too easy.
// Calculate product of all then for each index, divide total product by this value.
public static int[] CalcProductsWithDivision(int[] input)
{
int[] products = new int[input.Length];
int totalProduct = input.Length > 0 ? input.Aggregate((n, m) => n * m) : 1;
for (int i = 0; i < input.Length; ++i)
{
products[i] = totalProduct / input[i];
}
return products;
}
Solution 3: Use Both Sides
It took a while for my brain to understand you can split the problem in two and generate the left and right partial products separately. Hey, that’s clever! And it’s O(n). Well O(3n) but we can live with that right? But it’s using two extra arrays which isn’t good. Ok swap memory for runtime but maybe it can be better.
public static int[] CalcProductsFromLeftRightProducts(int[] input)
{
if ( input.Length == 0)
{
return input;
}
// products of all entries to left of each index
var leftProducts = CalcLeftProducts(input);
// products of all entries to right of each index
var rightProducts = CalcRightProducts(input);
// multiply left and right products to get product of all entries except that at each index
return leftProducts.Zip(rightProducts, (n, m) => n * m).ToArray();
}
private static int[] CalcLeftProducts(int[] input)
{
int[] leftProducts = new int[input.Length];
int partialProduct = 1;
leftProducts[0] = partialProduct;
for (int i = 1; i < input.Length; ++i)
{
partialProduct *= input[i-1];
leftProducts[i] = partialProduct;
}
return leftProducts;
}
private static int[] CalcRightProducts(int[] input)
{
int[] rightProducts = new int[input.Length];
int partialProduct = 1;
rightProducts[input.Length-1] = partialProduct;
for (int i = input.Length-2; i >= 0; --i)
{
partialProduct *= input[i+1];
rightProducts[i] = partialProduct;
}
return rightProducts;
}
Solution 4: Fast Right-Left Scan
So after more staring I did realise you don’t need all the left and right products in memory all the time as you don’t need anything but the original array to calculate each as you go. So you can calc the left products from left to right and then multiply in the right products in a single pass from right to left without any more memory. Time: O(2n), Memory used: single output array size n.
public static int[] CalcProductsWithFastRightLeftScan(int[] input)
{
if (input.Length == 0)
{
return input;
}
int[] products = new int[input.Length];
// from left-to-right calculate products of all entries to left of each index
CalcLeftProducts(input, products);
// from right-to-left multiply in products of all entries to right of each index
CombineRightProducts(input, products);
return products;
}
void CalcLeftProducts(int[] p, int[] products)
{
int partialProduct = 1;
products[0] = partialProduct;
for (int i = 1; i < p.Length; ++i)
{
partialProduct *= p[i - 1];
products[i] = partialProduct;
}
}
private static void CombineRightProducts(int[] p, int[] products)
{
int partialProduct = 1;
products[products.Length-1] *= partialProduct;
for (int i = products.Length - 2; i >= 0; --i)
{
partialProduct *= p[i+1];
products[i] *= partialProduct;
}
}
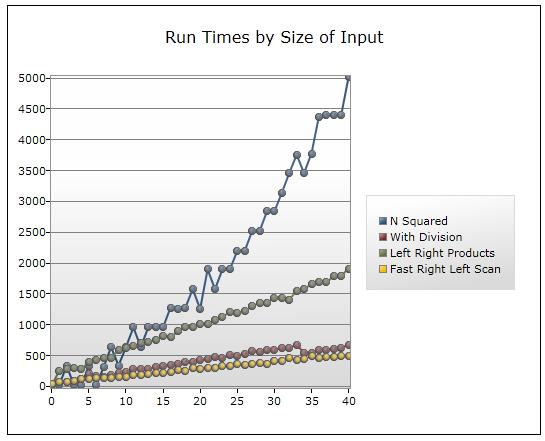
And here are the timing test results showing that yes, Solution 1 gets quite slow, and Solution 4 is the fastest.
I’m sure this is a well-known algorithm to some and there may be an even better solution. Please comment if you know.
What I was interested by was how I immediately attacked individual parts of the problem. Hearing “O(n)”, I could see easy O(n^2) solution. “no division”, try it with division. Only once I felt I understood the reason for individual words could I start to see the whole problem again. And only once it worked did I try and save space. Apparently I’ve internalised the advice against early optimisation.
No Comments